高考函数知识点总结,高考函数复习

复合函数

[编辑本段]

有3个变量，y是u的函数，y＝ψ（u），u是x的函数，u＝f（x），往往能形成链：y通过中间变量u构成了x的函数：

x→u→y，这要看定义域：设ψ的定义域为U 。 f的值域为U，当U*?U时，称f与ψ 构成一个复合函数 ， 例如 y＝lgsinx，x∈（0，π）。此时sinx＞0 ，lgsinx有意义 。但如若规定x∈（－π，0），此时sinx＜0 ，lgsinx无意义 ，就成不了复合函数。

反函数

[编辑本段]

就关系而言，一般是双向的 ，函数也如此 ，设y＝f（x）为已知的函数，若对每个y∈Y，有唯一的x∈X，使f（x）＝y，这是一个由y找x的过程 ，即x成了y的函数 ，记为x＝f -1（y）。称f -1为f的反函数。习惯上用x表示自变量 ，故这个函数仍记为y＝f -1（x） ，例如 y＝sinx与y＝arcsinx 互为反函数。在同一坐标系中，y＝f（x）与y＝f -1（x）的图形关于直线y＝x对称。

隐函数

[编辑本段]

若能由函数方程 F（x，y）＝0 确定y为x的函数y＝f（x），即F（x，f（x））≡0，就称y是x的隐函数。

思考：隐函数是否为函数？因为在其变化的过程中并不满足“一对一”和“多对一”

多元函数

[编辑本段]

设点（x1，x2，…，xn） ∈G?Rn，U?R1 ，若对每一点（x1，x2，…，xn）∈G，由某规则f有唯一的 u∈U与之对应：f：G→U，u＝f（x1，x2，…，xn），则称f为一个n元函数，G为定义域，U为值域。

基本初等函数及其图像 幂函数、指数函数、对数函数、三角函数、反三角函数称为基本初等函数。

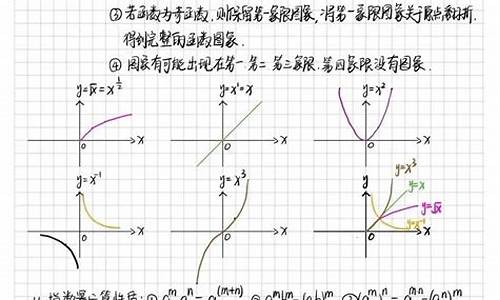
①幂函数：y＝xμ（μ≠0，μ为任意实数）定义域：μ为正整数时为（－∞，＋∞），μ为负整数时是（－∞，0）∪（0，＋∞）；μ＝(α为整数)，当α是奇数时为（ －∞，＋∞），当α是偶数时为（0，＋∞）；μ＝p／q,p,q互素，作为的复合函数进行讨论。略图如图2、图3。

②指数函数：y＝ax（a＞0 ，a≠1），定义成为（ －∞，＋∞），值域为（0 ，＋∞），a＞0 时是严格单调增加的函数（ 即当x2＞x1时，） ，0＜a＜1 时是严格单减函数。对任何a，图像均过点（0，1），注意y＝ax和y＝（）x的图形关于y轴对称。如图4。

③对数函数：y＝logax（a＞0）， 称a为底 ， 定义域为（0，＋∞），值域为（－∞，＋∞） 。a＞1 时是严格单调增加的，0＜a＜1时是严格单减的。不论a为何值，对数函数的图形均过点（1，0），对数函数与指数函数互为反函数 。如图5。

以10为底的对数称为常用对数 ，简记为lgx 。在科学技术中普遍使用的是以e为底的对数，即自然对数，记作lnx。

④三角函数：见表2。

正弦函数、余弦函数如图6，图7所示。

⑤反三角函数：见表3。双曲正、余弦如图8。

⑥双曲函数：双曲正弦（ex－e-x），双曲余弦?（ex＋e-x），双曲正切（ex－e-x）／（ex＋e-x） ，双曲余切（ ex＋e-x）／（ex－e-x）。

[编辑]补充

在数学领域，函数是一种关系，这种关系使一个集合里的每一个元素对应到另一个（可能相同的）集合里的唯一元素（这只是一元函数f（x）＝y的情况，请按英文原文把普遍定义给出，谢谢）。函数的概念对于数学和数量学的每一个分支来说都是最基础的。

术语函数，映射，对应，变换通常都是同一个意思。

二次函数

[编辑本段]

一般地，自变量x和因变量y之间存在如下关系：

y=ax^2+bx+c

（a，b，c为常数，a≠0，且a决定函数的开口方向，a>0时，开口方向向上，a<0时，开口方向向下。IaI还可以决定开口大小,IaI越大开口就越小,IaI越小开口就越大。）

则称y为x的二次函数。

二次函数表达式的右边通常为二次三项式。

x是自变量，y是x的函数

二次函数的三种表达式

一般式：y=ax^2+bx+c（a，b，c为常数，a≠0）

顶点式：y=a(x-h)^2+k [抛物线的顶点P（h，k）] 对于二次函数y=ax^2+bx+c 其顶点坐标为 (-b/2a,(4ac-b^2)/4a)</CA>

交点式：y=a(x-x?)(x-x ?) [仅限于与x轴有交点A（x? ，0）和 B（x?，0）的抛物线]

其中x1，2= -b±√b^2－4ac

注：在3种形式的互相转化中，有如下关系:

______

h=-b/2a k=(4ac-b^2)/4a x?,x?=(-b±√b^2-4ac)/2a

二次函数的图像

在平面直角坐标系中作出二次函数y=x^2的图像，

可以看出，二次函数的图像是一条抛物线。

抛物线的性质

1.抛物线是轴对称图形。对称轴为直线x = -b/2a。

对称轴与抛物线唯一的交点为抛物线的顶点P。

特别地，当b=0时，抛物线的对称轴是y轴（即直线x=0）

2.抛物线有一个顶点P，坐标为P ( -b/2a ，(4ac-b^2)/4a )

当-b/2a=0时，P在y轴上；当Δ= b^2-4ac=0时，P在x轴上。

3.二次项系数a决定抛物线的开口方向和大小。

当a＞0时，抛物线向上开口；当a＜0时，抛物线向下开口。

|a|越大，则抛物线的开口越小。

4.一次项系数b和二次项系数a共同决定对称轴的位置。

当a与b同号时（即ab＞0），对称轴在y轴左；

当a与b异号时（即ab＜0），对称轴在y轴右。

5.常数项c决定抛物线与y轴交点。

抛物线与y轴交于（0，c）

6.抛物线与x轴交点个数

Δ= b^2-4ac＞0时，抛物线与x轴有2个交点。

Δ= b^2-4ac=0时，抛物线与x轴有1个交点。

_______

Δ= b^2-4ac＜0时，抛物线与x轴没有交点。X的取值是虚数（x= -b±√b^2－4ac 的值的相反数，乘上虚数i，整个式子除以2a）

当a>0时，函数在x= -b/2a处取得最小值f(-b/2a)=4ac-b^2/4a；在{x|x<-b/2a}上是减函数，在{x|x>-b/2a}上是增函数；抛物线的开口向上；函数的值域是{x|x≥4ac-b^2/4a}相反不变

当b=0时，抛物线的对称轴是y轴，这时，函数是偶函数，解析式变形为y=ax^2+c(a≠0)

二次函数与一元二次方程

特别地，二次函数（以下称函数）y=ax^2+bx+c，

当y=0时，二次函数为关于x的一元二次方程（以下称方程），

即ax^2+bx+c=0

此时，函数图像与x轴有无交点即方程有无实数根。

函数与x轴交点的横坐标即为方程的根。

1．二次函数y=ax^2，y=a(x-h)^2，y=a(x-h)^2 +k，y=ax^2+bx+c(各式中，a≠0)的图象形状相同，只是位置不同，它们的顶点坐标及对称轴如下表：

解析式

y=ax^2

y=a(x-h)^2

y=a(x-h)^2+k

y=ax^2+bx+c

顶点坐标

(0，0)

(h，0)

(h，k)

(-b/2a，sqrt[4ac-b^2]/4a)

对 称 轴

x=0

x=h

x=h

x=-b/2a

当h>0时，y=a(x-h)^2的图象可由抛物线y=ax^2向右平行移动h个单位得到，

当h<0时，则向左平行移动|h|个单位得到．

当h>0,k>0时，将抛物线y=ax^2向右平行移动h个单位，再向上移动k个单位，就可以得到y=a(x-h)^2 +k的图象；

当h>0,k<0时，将抛物线y=ax^2向右平行移动h个单位，再向下移动|k|个单位可得到y=a(x-h)^2+k的图象；

当h<0,k>0时，将抛物线向左平行移动|h|个单位，再向上移动k个单位可得到y=a(x-h)^2+k的图象；

当h<0,k<0时，将抛物线向左平行移动|h|个单位，再向下移动|k|个单位可得到y=a(x-h)^2+k的图象；

因此，研究抛物线 y=ax^2+bx+c(a≠0)的图象，通过配方，将一般式化为y=a(x-h)^2+k的形式，可确定其顶点坐标、对称轴，抛物线的大体位置就很清楚了．这给画图象提供了方便．

2．抛物线y=ax^2+bx+c(a≠0)的图象：当a>0时，开口向上，当a<0时开口向下，对称轴是直线x=-b/2a，顶点坐标是(-b/2a，[4ac-b^2]/4a)．

3．抛物线y=ax^2+bx+c(a≠0)，若a>0，当x ≤ -b/2a时，y随x的增大而减小；当x ≥ -b/2a时，y随x的增大而增大．若a<0，当x ≤ -b/2a时，y随x的增大而增大；当x ≥ -b/2a时，y随x的增大而减小．

4．抛物线y=ax^2+bx+c的图象与坐标轴的交点：

(1)图象与y轴一定相交，交点坐标为(0，c)；

(2)当△=b^2-4ac>0，图象与x轴交于两点A(x?，0)和B(x?，0)，其中的x1,x2是一元二次方程ax^2+bx+c=0

(a≠0)的两根．这两点间的距离AB=|x?-x?| 另外，抛物线上任何一对对称点的距离可以由|2×（-b/2a）－A |（A为其中一点）

当△=0．图象与x轴只有一个交点；

当△<0．图象与x轴没有交点．当a>0时，图象落在x轴的上方，x为任何实数时，都有y>0；当a<0时，图象落在x轴的下方，x为任何实数时，都有y<0．

5．抛物线y=ax^2+bx+c的最值：如果a>0(a<0)，则当x= -b/2a时，y最小(大)值=(4ac-b^2)/4a．

顶点的横坐标，是取得最值时的自变量值，顶点的纵坐标，是最值的取值．

6．用待定系数法求二次函数的解析式

(1)当题给条件为已知图象经过三个已知点或已知x、y的三对对应值时，可设解析式为一般形式：

y=ax^2+bx+c(a≠0)．

(2)当题给条件为已知图象的顶点坐标或对称轴时，可设解析式为顶点式：y=a(x-h)^2+k(a≠0)．

(3)当题给条件为已知图象与x轴的两个交点坐标时，可设解析式为两根式：y=a(x-x?)(x-x?)(a≠0)．

7．二次函数知识很容易与其它知识综合应用，而形成较为复杂的综合题目。因此，以二次函数知识为主的综合性题目是中考的热点考题，往往以大题形式出现．

中考典例

1．(北京西城区)抛物线y=x2-2x+1的对称轴是( )

(A)直线x=1 (B)直线x=-1 (C)直线x=2 (D)直线x=-2

考点：二次函数y=ax2+bx+c的对称轴．

评析：因为抛物线y=ax2+bx+c的对称轴方程是：y=-，将已知抛物线中的a=1，b=-2代入，求得x=1，故选项A正确．

另一种方法：可将抛物线配方为y=a(x-h)2+k的形式，对称轴为x=h，已知抛物线可配方为y=(x-1)2，所以对称轴x=1，应选A．

2．( 北京东城区)有一个二次函数的图象，三位学生分别说出了它的一些特点：

甲：对称轴是直线x=4；

乙：与x轴两个交点的横坐标都是整数；

丙：与y轴交点的纵坐标也是整数，且以这三个交点为顶点的三角形面积为3．

请你写出满足上述全部特点的一个二次函数解析式： ．

考点：二次函数y=ax2+bx+c的求法

评析：设所求解析式为y=a(x-x1)(x-x2)，且设x1＜x2，则其图象与x轴两交点分别是A(x1，0)，B(x2，0)，与y轴交点坐标是(0，ax1x2).

∵抛物线对称轴是直线x=4，

∴x2-4=4 - x1即：x1+ x2=8 ①

∵S△ABC=3，∴(x2- x1)·|a x1 x2|= 3，

即：x2- x1= ②

①②两式相加减，可得：x2=4+，x1=4-

∵x1，x2是整数，ax1x2也是整数，∴ax1x2是3的约数，共可取值为：±1，±3。

当ax1x2=±1时，x2=7，x1=1，a=±

当ax1x2=±3时，x2=5，x1=3，a=±

因此，所求解析式为：y=±(x-7)(x-1)或y=±(x-5)(x-3)

即：y=x2-x+1 或y=-x2+x-1 或y=x2-x+3 或y=-x2+x-3

说明：本题中，只要填出一个解析式即可，也可用猜测验证法。例如：猜测与x轴交点为A(5，0)，B(3，0)。再由题设条件求出a，看C是否整数。若是，则猜测得以验证，填上即可。

5．( 河北省)如图13-28所示，二次函数y=x2-4x+3的图象交x轴于A、B两点，交y轴于点C，则△ABC的面积为( )

A、6 B、4 C、3 D、1

考点：二次函数y=ax2+bx+c的图象及性质的运用。

评析：由函数图象可知C点坐标为(0，3)，再由x2-4x+3=0可得x1=1，x2=3所以A、B两点之间的距离为2。那么△ABC的面积为3，故应选C。

图13-28

6．( 安徽省)心理学家发现，学生对概念的接受能力y与提出概念所用的时间x(单位：分)之间满足函数关系：y=-0.1x2+2.6x+43(0＜x＜30)。y值越大，表示接受能力越强。

(1)x在什么范围内，学生的接受能力逐步增强？x在什么范围内，学生的接受能力逐步降低？

(2)第10分时，学生的接受能力是什么？

(3)第几分时，学生的接受能力最强？

考点：二次函数y=ax2+bx+c的性质。

评析：将抛物线y=-0.1x2+2.6x+43变为顶点式为：y=-0.1(x-13)2+59.9，根据抛物线的性质可知开口向下，当x≤13时，y随x的增大而增大，当x>13时，y随x的增大而减小。而该函数自变量的范围为：0≤x≤30，所以两个范围应为0≤x≤13；13≤x≤30。将x=10代入，求函数值即可。由顶点解析式可知在第13分钟时接受能力为最强。解题过程如下：

解：(1)y=-0.1x2+2.6x+43=-0.1(x-13)2+59.9

所以，当0≤x≤13时，学生的接受能力逐步增强。

当13＜x≤30时，学生的接受能力逐步下降。

(2)当x=10时，y=-0.1(10-13)2+59.9=59。

第10分时，学生的接受能力为59。

(3)x=13时，y取得最大值，

所以，在第13分时，学生的接受能力最强。

9．( 河北省)某商店经销一种销售成本为每千克40元的水产品．据市场分析，若按每千克50元销售，一个月能售出500千克；销售单价每涨1元，月销售量就减少10千克．针对这种水产品的销售情况，请解答以下问题：

(1)当销售单价定为每千克55元时，计算月销售量和月销售利润；

(2)设销售单价为每千克x元，月销售利润为y元，求y与x的函数关系式(不必写出x的取值范围)；

(3)商店想在月销售成本不超过10000元的情况下，使得月销售利润达到8000元，销售单价应定为多少？

解：(1)当销售单价定为每千克55元时，月销售量为：500–(55–50)×10=450(千克)，所以月销售利润为

:(55–40)×450=6750(元)．

(2)当销售单价定为每千克x元时，月销售量为：[500–(x–50)×10]千克而每千克的销售利润是:(x–40)元，所以月销售利润为：

y=(x–40)[500–(x–50)×10]=(x–40)(1000–10x)=–10x2+1400x–40000(元)，

∴y与x的函数解析式为：y =–10x2+1400x–40000．

(3)要使月销售利润达到8000元，即y=8000，∴–10x2+1400x–40000=8000，

即：x2–140x+4800=0，

解得：x1=60，x2=80．

当销售单价定为每千克60元时，月销售量为：500–(60–50)×10=400(千克)，月销售成本为：

40×400=16000(元)；

当销售单价定为每千克80元时，月销售量为：500–(80–50)×10=200(千克)，月销售单价成本为：

40×200=8000(元)；

由于8000＜10000＜16000，而月销售成本不能超过10000元，所以销售单价应定为每千克80元．